CART

Ahmad Mu’allal Hifni – 17106050034

CART (Classification and Regression Trees) merupakan salah satu metode atau algoritma dari teknik pohon keputusan (decision tree). Metode yang dikembangkan oleh Leo Breiman, Jerome H. Friedman, Richard A. Olshen, dan Charles J.

Metode CART terdiri dari dua metode yaitu pohon klasifikasi dan metode regression. Jika variabel dependen yang dimiliki bertipe kategorik maka CART menghasilkan pohon klasifikasi (classification trees). Sedangkan jika variabel dependen yang dimiliki bertipe kontinu atau numerik maka CART menghasilkan pohon regresi (regression trees).

Data Mining – Supervised – Klasifikasi – Decision Tree – CART

Contoh Perhitungan Menggunakan Algoritma CART

Asal Sekolah (SMA/MA/SMK) NEM(Bahasa, Matematika, B Ing SMA) IPK (Informatika)

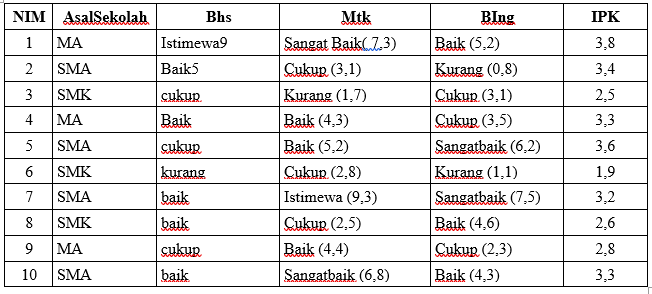
Istimewa : 8-10                                                Mengecewakan : 3-4
sangat baik      : 6-8 Memuaskan : 0-3
baik                 : 4-6
cukup              :2-4
kurang             : 0-2

Gini = 1 – Σ (Pi)² for i=1 to number of classes

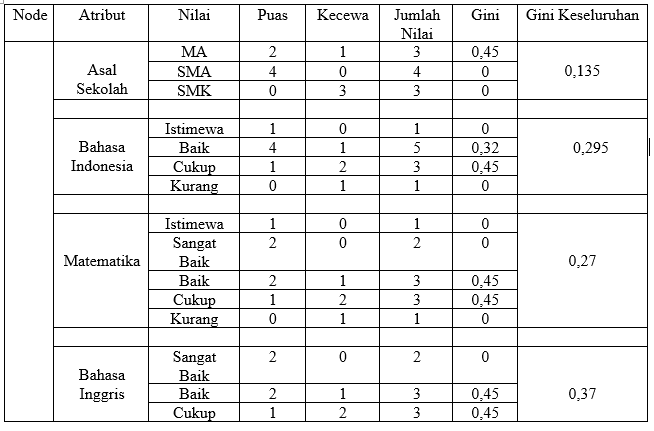
Asal Sekolah :

MA      = 1 – (2/3)^2 – (1/3)^2             = 1 – (0,44) – (0,11)             = 0,45	SMK   = 1 – (0/3)^2 – (3/3)^2             = 1 – (0) – (1)             = 0
SMA   = 1 – (4/4)^2 – (0/4)^2             = 1 – (1) – (0)             = 0	Gini Asal Sekolah = (3/10)*0,45 + (4/10)*0 + (3/10)*0                           = (0,135 ) + 0 + 0                           = 0,135

Bahasa Indonesia :

Istimewa = 1 – (1/1)^2 – (0/1)^2                = 1 – (1) – (0)                = 0	Kurang            = 1 – (0/1)^2 – (1/1)^2             = 1 – (0) – (1)             = 0
Baik     = 1 – (4/5)^2 – (1/5)^2             = 1 – (0,64) – (0,04)             = 0,32	Gini Bahasa        = (1/10)*0 + (5/10)*0,32 + (3/10)*0,45 + (1/10)*0                         = 0 + 0,16 + 0,135 + 0                         = 0,295
Cukup = 1 – (1/3)^2 – (2/3)^2             = 1 – (0,11) – (0,44)             = 0,45

Matematika :

Istimewa = 1 – (1/1)^2 – (0/1)^2               = 1 – (1) – (0)              = 0	Cukup = 1 – (1/3)^2 – (2/3)^2             = 1 – (0,11) – (0,44)             = 0,45
Sangat Baik = 1 – (2/2)^2 – (0/2)^2                    = 1 – (1) – (0)                   = 0	Kurang            = 1 – (0/1)^2 – (1/1)^2             = 1 – (0) – (1)             = 0
Baik     = 1 – (2/3)^2 – (1/3)^2             = 1 – (0,44) – (0,11)             = 0,45	Gini Matematika         = (1/10)*0 + (2/10)*0 + (3/10)*0,45 + (3/10)*0,45 + (1/10)*0 = (0) + (0) + (0,135) + (0,135) + (0) = 0,27

Bahasa Inggris :

Sangat Baik     = 1 – (2/2)^2 – (0/2)^2                         = 1 – (1) – (0)                         = 0	Kurang            = 1 – (1/2)^2 – (1/2)^2             = 1 – (0,25) – (0,25)             = 0,5
Baik     = 1 – (2/3)^2 – (1/3)^2             = 1 – (0,44) – (0,11)             = 0,45	Gini Bahasa Inggris = (2/10)*0 + (3/10)*0,45 + (3/10)*0,45 + (2/10)*0,5 = (0) + (0,135) + (0,135) + (0,1) = 0,37
Cukup = 1 – (1/3)^2 – (2/3)^2             = 1 – (0,11) – (0,44)             = 0,45

Mencari Root Atribut :

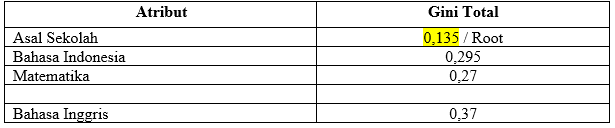
Dikarenakan SMA dan SMK telah **** tidak mempunyai leaf, maka tidak perlu mencari nilai GINI, sedangkan MA mempunyai **** yang berbeda sehingga dicari nilai GINI nya.

Bahasa Indonesia

Matematika

Bahasa Inggris

Mencari Root Bahasa :

Desision Tree :

Data UJI :

Data uji dalam label :

Hasil perhitungan : akurasi, presisi, recall :

Sumber:
– Data Mining. Concepts and Techniques, 3rd Edition (The Morgan Kaufmann Series in Data Management Systems).
– Penggunaan Metode Classification and Regression Trees (CART) untuk Klasifikasi Rekurensi Pasien Kanker Serviks di RSUD Dr. Soetomo Surabaya oleh Siti Holis Sumartini dan Santi Wulan Purnami.